Coframe
It is dual to frame on a manifold.
It is an ordered set of 1-forms $\{\theta^1,\ldots,\theta^m\}$ defined on an open set $U$ of an $m$-dimensional manifold $M$ such that they span the cotangent space $T_x M$ for every $x\in U$.
An ordered set $\{\theta^1,\ldots,\theta^m\}$ define a coframe if and only if
$$ \theta^1 \wedge \ldots \wedge\theta^m\neq 0 $$for every $x\in U$ ([Olver_1995]).
A global coframe provides, therefore, an orientation and a trivialization o $T^* M\approx M\times \mathbb{R}^m$, so it is also called absolut paralelism.
Generation of k-forms
A coframe $\{\theta^1,\ldots,\theta^m\}$ not only generate any 1-form, but also any differential $k$-form can be written as linear combination of $k$-fold wedge products:
$$ \sum_{I} h_{I}(x) \theta^{i_{1}} \wedge \cdots \wedge \theta^{i_{k}} $$See [Olver_1995] page 254.
Duality with frames
A frame on a manifold and a coframe are dual if they are dual basis for every $x\in U$. Given a coframe, the dual frame will be denoted by
$$ \frac{\partial}{\partial \theta^j} $$Given coordinates $(x_1\ldots,x_m)$ on the manifold, we have distinguished local frame and coframe denoted respectively by
$$ \{\frac{\partial}{\partial x^1},\ldots, \frac{\partial}{\partial x^m} \} $$and
$$ \{dx^1,\ldots,dx^m\}. $$Given a coframe $\{\theta^1,\ldots,\theta^m\}$ any $k$-form $\Omega$ can be written as a linear combination
$$ \Omega=\sum_{I} h_{I}(x) \theta^{i_{1}} \wedge \cdots \wedge \theta^{i_{k}}. $$In particular,
$$ d \theta^{i}=\sum_{j, k=1 \atop j([Olver 1995]). This relation is proved by the infinitesimal Stokes' theorem.
Visualization
(where we are calling $e_j$ to $\frac{\partial}{\partial \theta^{j}}$):
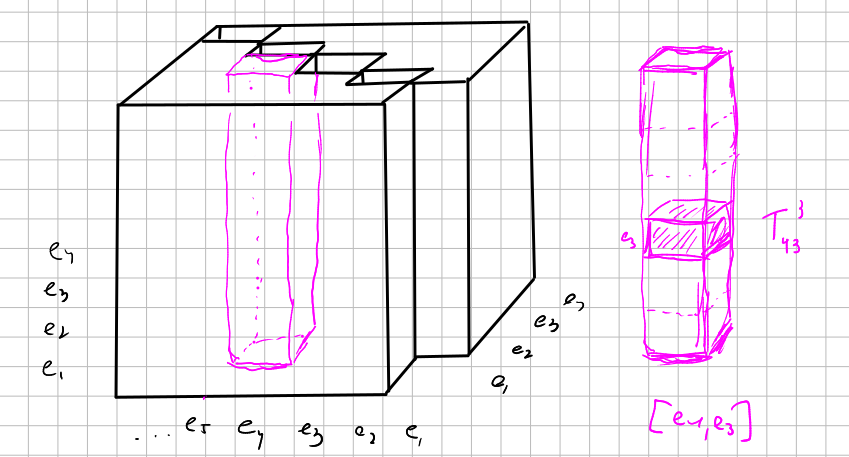
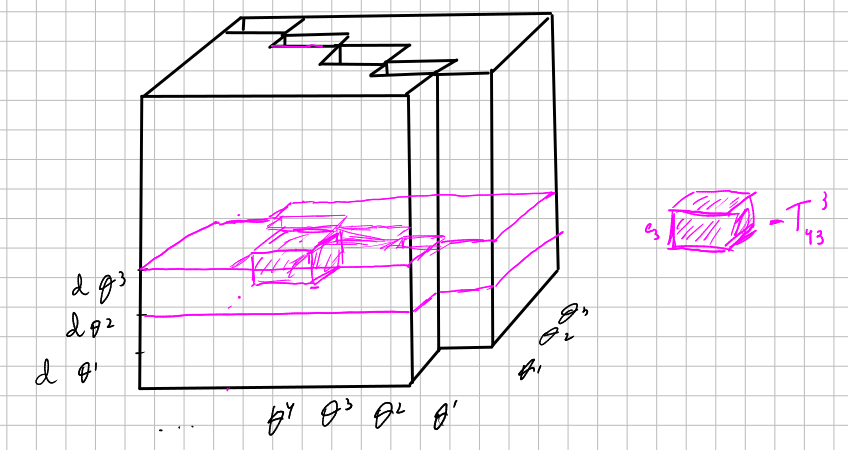
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: